Reminder: This post contains 4022 words
· 12 min read
· by Xianbin
What is Determinant?
In Wiki, it says that
In mathematics the determinant is a scalar-valued function of the entries of a square matrix.
In Geometry, Determinant is a Volume
Since it is a volume, the output must be a value!
Let us put it more simple. Determinant is function f: Rn×⋯×Rn→R.
Let a1,a2 be vectors of size two.
f(a1,a2)=Det(a1,a2)
If we increase a1 to be ca1 where c>1, then the volume increases c times.
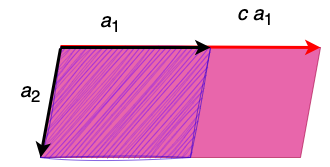
1):f(ca1,a2)=cf(a1,a2)
That is simple, right?
By similar tricks, we have that
2):f(a1+v,a2)=f(a1,a2)+f(v,a2)
Now, let us consider the exchange of two vectors in f.
f(a1,…,ak,…,ai,…,an)
We know that the absolute value cannot change. Notice that due to the definition of determinant, the notion sign will change.
Then,
3):f(a1,…,ak,…,ai,…,an)=−f(a1,…,ai,…,ak,…,an)
Finally, we know that if the vectors all unit vectors, we have
(4)f(e1,…,ei,…,ek,…,en)=1
where ei⊥ej for any i=j.
That is because, the volume can only be one.
Now, let us see Det(a1,a2). By property (1),(2),(3),(4).
Det(a1,a2)=Det((v2v1),(v4v3))=Det((0v1)+(v20),(v4v3))=Det((0v1),(v4v3))+Det((v20),(v4v3))=v1Det((01),(v4v3))+v2Det((10),(v4v3))=v1v3Det((01),(01))+v1v4Det((01),(10))+v2v3Det((10),(01))+v2v4Det((10),(10))=v1v4−v2v3
Let us calculate Det(a1,…,an).
Det⎝⎛⎝⎛v11⋮vn1⎠⎞⎝⎛v12⋮vn2⎠⎞,⋯,⎝⎛vn1⋮vn1⎠⎞⎠⎞=Det(v11e1+…,vn1en,Δ1)=v11Det(e1,Δ1)+…+vn1Det(en,Δ1)=j1=1∑nvj1,1Det(ej1,Δ1)
where
Δ1=⎝⎛⎝⎛vn2⋮vn2⎠⎞,⋯,⎝⎛vn1⋮vn1⎠⎞⎠⎞
Now, we obtain a recursion equality.
Det(a1,Δ1)=j1=1∑nvj1,1Det(ej1,Δ1)
We can see that the relationship is this:
First, we swap a2 to ej1, then, we have
Det(a1,a2,Δ2)=j1=1∑nvj1,1Det(a2,ej1,Δ2)⋅(−1)=j1=1∑nj2=1∑nvj1,1vj2,2Det(ej2,ej1,Δ2)⋅(−1)
Then, we swap it back.
Det(a1,Δ1)=Det(a1,a2,Δ2)=j1=1∑nj2=1∑nvj1,1vj2,2Det(ej1,ej2,Δ2)⋅(−1)⋅(−1)=j1=1∑nj2=1∑nvj1,1vj2,2Det(ej1,ej2,Δ2)
We construct Δn−1⊂⋯⊂Δ1 such that Δi+1∪ai+1=Δi, where Δn−1=ejn and i∈[n−2].
Then, we have
Det(a1,a2,…,an)=j1=1∑nj2=1∑n…jn=1∑nvj1,1…vjn,nDet(ej1,…,Δn−1)=δ=(j1,…,jn)∈πn∑sgn(j1,…,jn)i=1∏nvjδ(i),i
where πn is a permutation of {1,…,n}.
Reference
[1] The Bright Side of Mathematics. Linear Algebra 45,46.
