C1: Combinatorial Correlation Clustering

April 10, 2024

• Efficient MPC Algorithms for Correlation Clustering
  • Algorithm 1 (Basic 2-approximation local search algorithm)
  • An improved version of 15/8-approximation
    • The Process:
  • A Complex Version
• Reference

This post is based on [1].

Efficient MPC Algorithms for Correlation Clustering

Local Search is a powerful method for clustering problems. Again, this tool shows us its strength in correlation clustering.

Algorithm 1 (Basic 2-approximation local search algorithm)

Let $S$ be the solution output by the algorithm and let OPT be the optimum solution.

  For each cluster C in OPT, 
             1) Consider S_C that is by inserting C 
             into S as a cluster and removing 
             elements from S. 
             2) Update S by inserting S_, reducing the cost.

The naive way of finding the $S_C$ is using an exponential algorithm. Now, let us forget how to obtain $S_C$ first and focus on the approximation ratio.

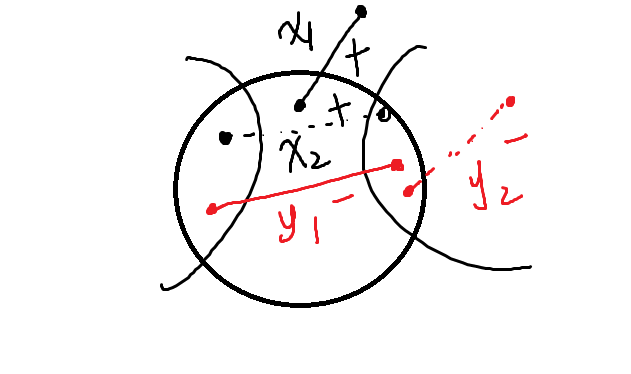
In the above picture, we use $x_1, x_2$ with signal $+$ to denote the increased cost by inserting $C$ into $S$ (for the nodes in $C$). We use $y_1, y_2$ with signal $-$ to denote the saved cost by inserting $C$ into $S$ (for nodes in $C$). Let $comm$ to denote the common cost between the the optimal algorithm and an algorithm.

Due to local optimality, (it means that we cannot reduce the cost by inserting $C$), we have that

$$comm + x_1 + x_2 \geq comm + y_1 + y_2$$

We use $cost(OPT)$ to denote the optimum cost and use $cost(S)$ to denote the cost of an algorithm. Now, we get that

$$cost(OPT) = \sum_C comm+x_1/2 + x_2$$ $$cost(S) = \sum_C comm+y_1 + y_2/2$$

Then, we have

$$\begin{aligned} cost(S) \leq \sum_C comm+y_1 + y_2 & \\ \leq \sum_C comm+x_1+x_2 & \\ \leq 2(\sum_C comm + x_1/2 + x_2) &\\ =2\cdot cost(OPT). \end{aligned}$$

An improved version of 15/8-approximation

Let $Alg_i$ be a local optimum clustering with weights $w_i$.

The Process:

1. Set $Algo_1$ with weight function $w_1$;

2. Double the weight of edges in $E^+ \cap EXT(Alg_1)$ to get a new weight function $w_2$ where $EXT(?)$ is the edges across clusters.

3. Set $Algo_2$ with weight function $w_2$;

4. Output the best of $Algo_1$ and $Algo_2$.

A Complex Version

---

$\color{red} \text{To be continued \ldots}$

Reference

[1]. Combinatorial Correlation Clustering, Vincent Cohen-Addad, David Rasmussen Lolck, Marcin Pilipczuk, Mikkel Thorup, Shuyi Yan, and Hanwen Zhang. Proceedings of the Symposium on Theory of Computing (STOC) 2024.