Reminder: This post contains 4145 words
· 12 min read
· by Xianbin
This post gives some basics about vector norms and matrix norms. After using those basic tools efficiently, we can do a lot of interesting things.
What is a norm?
A (vector) norm is a function \(v: \mathbb{C}^n \to \mathbb{R}\) such that for any \(x,y\in \mathbb{C}^n\) and \(\alpha \in \mathbb{C}\), we have
1) \(v\) is positive;
2) \(v\) is homogeneous, i.e., \(v(\alpha x) = \lvert \alpha \rvert v(x)\).
3) \(v\) satisfies triangle inequality, i.e., \(v(x+y) \leq v(x) + v(y)\).
Conjugate Transpose
-
\((A^H)^H = A\).
-
\((A+B)^H = A^H + B^H\).
-
\((AB)^H = B^HA^H\).
-
\((A^{-1})^H = (A^H)^{-1}\) (if invertible).
The proofs can be obtained by definitions. Here, we only prove (2).
\(\textbf{Proof}\) (2).
We know that,
\(\overline {a+b} = \bar{a} + \bar{b}.\)
\[(A+B)^H = (a_1+b_1,\ldots,a_n+b_n)^H=\\
\left(
\begin{matrix}
\overline {a_1+b_1};\\
\vdots\\
\overline {a_n+b_n};\\
\end{matrix}
\right)\\=
\left(
\begin{matrix}
\overline {a_1};\\
\vdots\\
\overline {a_n};\\
\end{matrix}
\right)+
\left(
\begin{matrix}
\overline {b_1};\\
\vdots\\
\overline {b_n};\\
\end{matrix}
\right)=\\
A^H + B^H\]
Vector 2-norm (Euclidean)
\(\textbf{Definition 1}\). The vector 2-norm is a function \(\mathbb{C}^n \to \mathbb{R}\). For a vector \(A\in \mathbb{C}^n\),
\[\left \lVert A\right \rVert_2 = \sqrt{A^HA} = \sqrt{\bar a_1 a_1+\cdots+\bar a_n a_n} = \sqrt{\lvert a_1 \rvert^2+\cdots + \lvert a_n \vert^2}\]
\(\textbf{Inner Product}\). For \(x,y\in \mathbb{C}^n\), we have
\(x^Ty=\sum_i^n x_iy_i \in \mathbb{R}\).
\(x^Hy = \sum_{i=1}^n \bar x_i y_i \in \mathbb{C}\).
Practice
\(\textbf{Theorem}\)[Cauchy-Bunyakovskii-Schwarz Inequality]. Let \(x,y \in \mathbb{C}^n\), we have
\[\lvert x^Hy \rvert \leq \left \lVert x \right \rVert_2 \left \lVert y\right \rVert_2\]
\(\textbf{Proof}\).
Let \(\alpha = \frac{x^Hy}{x^Hx}\).
\[\lVert \alpha x - y \rVert^2= \\
(\alpha x - y)^H(\alpha x - y)=\\
\alpha x^Hy - \bar \alpha x^Hy - \alpha y^Hx + y^Hy = - \alpha y^Hx + y^Hy \geq 0\]
Replace \(\alpha\), we obtain
\[y^Hy \cdot x^Hx \geq x^Hy \cdot y^Hx\]
Thus, we prove this theorem.
\(\textbf{Theorem}\). The vector 2-norm is a norm.
\(\textbf{Proof}\). It is easy to see that the vector 2-norm satisfies the first two properties. Now, let us prove the triangle property.
\[\lVert x + y \rVert_2^2 = (x+y)^H(x+y) \\ =
x^Hx + y^Hx+x^Hy + y^Hy\\ \leq
\lVert x \rVert^2_2 + 2\lVert x\rVert_2 \lVert y \rVert_2 + \lVert y \rVert_2^2 = (\lVert x \rVert_2 + \lVert y \rVert_2)^2\]
Matrix Norms
\(\textbf{Frobenius Matrix Norm}\). Given \(A \in \mathbb{C}^{m\times n}\) is as follows.
\[\lVert A \rVert_F^2 = \sum_{i,j}\lvert a_{i,j}\lvert^2 = \sum_i \sum_j \lvert a_{i,j} \rvert^2 = \sum_j\lVert A_{*j}\rVert^2_2\]
\(\textbf{lemma}\) Frobenius Matrix norm is a norm.
\(\textbf{Proof}\). By the definition, we know that
\[\lVert A \rVert_F= \sqrt{ \sum_j\lVert A_{*j}\rVert^2_2} = \sqrt{\sum_j \lvert X_j \rvert^2}\]
where
\[\lvert X_j \rvert = \lVert A_{*j} \rVert_2\]
Apparently, it is a vector 2-norm, so it is a norm.
The trace of a matrix \(A\) is the sum of diagonals of \(A\), i.e.,
\(\text{trace}(A) = \sum_{i=1}^n a_{ii}\).
\(\textbf{Lemma}\) Prove that for any \(A\in \mathbb{R}^{m\times n}\), \(\lVert A \rVert_F^2 =\text{trace}(AA^\intercal)\).
\(\textbf{Proof}\). Since \(A\in \mathbb{R}^{m\times n}\), \(A^H = A^\intercal\). Notice that
\[\text{trace}(AA^T) = \sum_{i=1}^m A_i A_i^\intercal = \sum_{i=1}^m A_i A_i^H= \sum_{i=1}^m \lVert A \rVert_F^2.\]
Induced Matrix Norms
This norm is interesting.
\[\lVert A \rVert_{u,v} = \text{sup}_{x\in \mathbb{C}^n, x\neq 0}\frac{\lVert Ax \rVert_\mu}{\lVert x \rVert_v}\]
\(\textbf{Lemma}\). \(\text{sup}_{x\in \mathbb{C}^n, x\neq 0}\frac{\lVert Ax \rVert_\mu}{\lVert x \rVert_v} = \text{sup}_{\lVert x \rVert_v = 1} \lVert Ax \rVert_u\)
\(\textbf{Proof}\). We know that \(\lVert \frac{x}{\lVert x \rVert_v} \rVert_v = \frac{\lVert x \rVert_v}{\lVert x \rVert_v} = 1.\)
Then,
\[\begin{align}
\begin{aligned}
\text{sup}_{x\in \mathbb{C}^n, x\neq 0}\frac{\lVert Ax \rVert_\mu}{\lVert x \rVert_v} = \text{sup}_{x\in \mathbb{C}^n, x\neq 0} \lVert \frac{Ax}{\lVert x \rVert_v}\rVert_u \\=
\text{sup}_{x\in \mathbb{C}^n, x\neq 0} \lVert A\frac{x}{\lVert x \rVert_v}\rVert_u = \text{sup}_{x\in \mathbb{C}^n, x\neq 0, y = \frac{x}{\lVert x \rVert_v}} \lVert A y\rVert_u \\= \text{sup}_{\lVert y\rVert_v = 1} \lVert Ay \rVert_u = \text{sup}_{\lVert x \rVert_v = 1} \lVert Ax \rVert_u
\end{aligned}
\end{align}\]
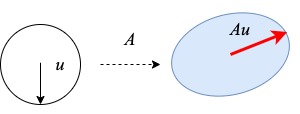
For the special case, \(u = 2\), \(\lVert A \rVert_2 = \max_{\lVert u \rVert_2} \lVert Au \rVert_2\) is called the spectral norm of a matrix \(A \in \mathbb{R}^{m\times n}\). The following illustration shows the definition well.
Reference
[1]. Linear Algebra: Foundations to Frontiers. A Collection of Notes on Numerical Linear Algebra. Robert A. van de Geijn