Reminder: This post contains 4643 words
· 14 min read
· by Xianbin
Yao’s minimax principle in Property Testing
For basics on Yao’s minimax principle, see this post.
\(\textbf{Theorem 1}\). Let \(\mathcal{P}\) be a property over a function \(f: [n] \to R\). Suppose for \(n\in \mathbb{Z}^+\), and \(\epsilon \in (0,1)\), there exists a distribution \(D\) over functions such that, for any deterministic algorithm \(\mathcal{A}\) that makes at most \(q(n,\epsilon)\) queries to the function, it holds
\[P_{f \sim \mathcal{D}}\left[\mathcal{A} \text{ errs in testing } \mathcal{P}\text{ on } (n,\epsilon, f)\right] > 1/3\]
Then, the query complexity to test \(\mathcal{P}\) on an error parameter \(\epsilon\) and a function \(f:[n] \to R\) is more than \(q(n,\epsilon)\).
Notice that if we only care about non-adaptive/one sided eror algorithms, the lower bounds hold to non-adaptive/one sided error testing.
\(\textbf{Corollary 1}\). Let \(p_1 = P_{f\in D_1}[A(n,\epsilon, f) = 1] \geq 1-\eta_1\) be the probability that \(f\sim D_1\) satisfies \(\mathcal{P}\). Let \(p_2 = P_{f\in D_1}[A(n,\epsilon, f) = 0] \geq 1-\eta_0\) be the probability that \(f\sim D_2\) \(\epsilon\)-far from \(\mathcal{P}\). For any deterministic algorithm \(\mathcal{A}\) that makes at most \(q(n,\epsilon)\) queries to the input function, we have
\[\lvert p_1 - p_2 \rvert \leq \eta_2.\]
If \(\sum_{i=1}^3 \eta_i < 1/3\), then the query complexity of testing \(\mathcal{P}\) on an error parameter \(\epsilon\) and a function \(f: [n] \to R\) is more than \(q(n,\epsilon)\).
Applications
1. Testing all-one strings.
Let \(L_{one} = \{1^n: n\in \mathbb{Z}^{+} \}\subseteq \{0,1\}^*\) be the language of all-one strings.
\(\textbf{Theorem}\). Any tester for \(L_{one}\) requires \(\Omega(\epsilon^{-1})\) queries.
\(\textbf{Proof}\). Let \(D_1\) be the function distribution which we always sample the all-one string. Next, we construct \(D_0\).
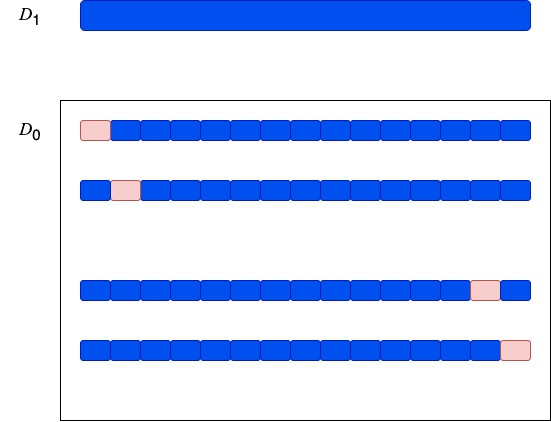
Divide \([n]\) into \(1/\epsilon\) blocks and flip 1 into 0 in one of the blocks. Then, we obtain \(1/\epsilon\) blocks shown above, i.e., \(b_1,\ldots,b_\epsilon\). Let \(D_0\) be the uniform distribution over the above blocks.
We can see that \(D_1\) satisfies \(L_{one}\) and \(D_0\) is \(\epsilon\)-far from \(L_{one}\). To apply Corollary 1, we need to prove that the gap between the probability is small. Let \(A\) denote a deterministic algorithm that queries at most \(o(1/\epsilon)\) indexes. Let \(p_1 = P_{s\in D_1}[A(n,\epsilon, s)=1]\) and \(p_2 = P_{s\in D_0}[A(n,\epsilon, s)=1]\).
Now matter how smart the algorithm \(A\) is, each block has a probability \(\epsilon\) having 0.
Then,
\[p_1 = 1;\\
p_2 = P_{s\in D_0}[A(n,\epsilon, s)=1] \geq (1-\epsilon)^{\lvert S\rvert} > 2/3\]
where \(S\) is the set of queried indexes, \(\lvert S \rvert = o(1/\epsilon)\). (The reason why we set \(\lvert S \rvert\) is that we will show the lower bound is \(\omega(\lvert S\rvert) = \Theta(\epsilon))\).
Then,
\[\lvert p_1 - p_2 \rvert < 1/3\]
By Corollary 1, it is proved.
2. Testing Monotonicity on a Hypercube
\(\textbf{Theorem}\). For any one-sided error non-adaptive tester for monotonicity of functions \(f:\{0,1\}\to \{0,1\}\), it requires \(\Omega(\sqrt{n})\) quires.
\(\textbf{Proof}\). For this problem, the key is to understand the conceptions. For monotonicity, what is the \(\epsilon\)-far from the monotonicity? It means that there are at least \(\epsilon\) proportion of inputs have violations, i.e., for \(x < y\), \(f(x) \geq f(y)\).
Next, we define violating pairs and violating edges.
A pair \((x,y) \in \{0,1\}^n \times \{0, 1\}^n\) is a violating pair if \(x \leq y\) and \(f(x) > f(y)\). Further, \((x,y)\) is a \(\textit{violating edge}\) if \(\lVert x \rVert + 1 = \lVert y\rVert\).
Since our goal is to prove the lower bounds, we need to create two distributions that are not easy to distinguish.
Notice that in this problem, we need to check by at least two queries and then we may know the result. Also, recall the definition of monotonicity, if \(x<y\), then \(\lVert x \rVert < \lVert y \rVert\) (\(\lVert x \rVert = \sum \lvert x_i \rvert\)).
\[f_j(x_1,\ldots,x_n) =
\begin{cases}
1 && \lVert x \rVert < n/2 + \sqrt{n}\\
0 && \lVert x \rVert < n/2 - \sqrt{n} \\
1 - x_j && \text{middle-case}.
\end{cases}\]
Now, consider the following edge
\[(a,b)\]
where \(a = (x_1,\ldots, x_{j-1},0, x_{j+1},\ldots,x_n)\) and \(b = (x_1,\ldots, x_{j-1},1, x_{j+1},\ldots,x_n)\)
We can see that \((a,b)\) is a violating edge if and only if \(a, b\) are in the middle-case. Let us consider the size of middle-case. Since for each bit, there are only two possibilities, 0 or 1. We can consider that it is a random process in which 0 or 1 has probability 1/2. Then, by the Chernoff Bound, there are at least some \(\epsilon n\) violating edges, which means that each \(f_j\) is \(\epsilon\)-far from being monotone.
Next, we use the old trick. Let \(D\) be the uniform distribution over all \(f_j\).
Let \(A\) be a deterministic non-adaptive tester for monotonicity of functions \(f: \{0,1\}^n\to \{0,1\}\) with query complexity \(q\).
\(\textbf{Lemma}\). The probability that \(A\) detects a violating pair from \(D\) is at most \(O(q/\sqrt{n})\).
By Corollary 1, the gap between two probabilities is at most \(O(q/\sqrt{n})\). By setting \(q/\sqrt{n} = \epsilon'\), we can show that \(q = \Omega(\sqrt{n})\).
Reference
[1]. Bhattacharyya, A. and Yoshida, Y., 2022. Property Testing: Problems and Techniques. Springer Nature.